 Digitech III-2
Digitech III-2
Τοπογραφικές μέθοδοι
Η χρήση τοπογραφικών οργάνων και συγκεκριμένα θεοδόλιχων και αποστασιομέτρων για αποτύπωση σημείων του τρισδιάστατου χώρου έχειξεκινήσει από πολύ παλιά και μπορούμε να πούμε ότι η σημερινή τεχνολογίατων οργάνων μέτρησης είναι αρκετά ικανοποιητική ώστε να είναι σε θέση να αποτυπώνει με σημαντική ακρίβεια μετρήσεων αρχαιολογικά και αρχιτεκτονικά μνημεία.
Ωστόσο αν και η τοπογραφική αποτύπωση μπορεί να προσδιορίσει με τη μέγιστη δυνατή ακρίβεια τα σημεία ενός αντικειμένου στο χώρο υπολείπεται της φωτογραμμετρικής αποτύπωσης για τους παρακάτω λόγους:
- θα πρέπει να τηρείται στο πεδίο ένα αρκετά λεπτομερές σκαρίφημα-κροκί των μετρήσεων με σκοπό την πλήρη ανακατασκευή του μοντέλου στον Η/Υ που γίνεται με χειροκίνητο τρόπο. Το γεγονός αυτό καθιστά υπερβολικά χρονοβόρα τη διαδικασία των μετρήσεων ενός αντικειμένου και ταυτόχρονα αντιοικονομική λόγω του αυξημένου αριθμού των εργατοωρών των χειριστών των οργάνων.
- Ο προσδιορισμός των τρισδιάστατων συντεταγμένων των σημείων που προσδιορίζονται στο χώρο δεν οδηγούν άμεσα στην κατασκευή του τρισδιάστατου μοντέλου του μνημείου-χώρου. Περαιτέρω επεξεργασία σε ένα πακέτο τρισδιάστατης σχεδίασης πρέπει να ακολουθήσει, προκειμένου να συνδεθούν τα προσδιορισμένα σημεία στο χώρο, ώστε να σχηματιστούν τα επίπεδα των εξωτερικών επιφανειών που περιγράφουν το μνημείο-χώρο.
Τα όργανα μετρήσεων που μπορούν να χρησιμοποιηθούν και είναι σε θέση να ορίσουν ένα τρισδιάστατο σύστημα συντεταγμένων, στο οποίο αναφέρονται όλες οι μετρήσεις των σημείων, θα μπορούσαν να χαρακτηριστούν μέτριου κόστους (μέχρι 10.000€) και η χρήση τους πρέπει να γίνεται από έμπειρους μηχανικούς (συνήθους Αγρονόμους Τοπογράφους Μηχανικούς, Πολιτικούς Μηχανικούς ή Αρχιτέκτονες Μηχανικούς) ή τεχνολόγους. Το όργανο που κατά κόρον χρησιμοποιείται σήμερα στην τοπογραφική αποτύπωση είναι ο Γεωδαιτικός Σταθμός (Total Station) που αποτελεί την μετεξέλιξη του θεοδόλιχου (όργανο για τη μέτρηση των γωνιών) που είναι το παραδοσιακό όργανο για τη μέτρηση γωνιών και του ηλεκτρονικού αποστασιόμετρου (που συνδυάζεται με χρήση κάτοπτρων, ή άλλης ανακλαστικής επιφάνειας ή υπέρυθρης ακτίνας ή ακτίνας laser) για τη μέτρηση αποστάσεων.
Πολλές φορές η πολυπλοκότητα του αντικειμένου και η μεγάλη λεπτομέρεια που εμφανίζουν τα αρχιτεκτονικά και αρχαιολογικά μνημεία καθιστούν ασύμφορη οικονομικά αλλά και χρονικά την τοπογραφική μέθοδο αποτύπωσης. Για το λόγο αυτό μπορεί η τοπογραφική αποτύπωση να συνδυαστεί με την φωτογραμμετρική μεθοδολογία ώστε να ληφθούν μόνο οι ελάχιστες τοπογραφικές μετρήσεις (μέτρηση φωτοσταθερών) που είναι απαραίτητες για τον καθορισμό του επίγειου τρισορθογώνιου συστήματος συντεταγμένων στο οποίο θα αναφερθούν οι φωτογραφίες των στερεομοντέλων που θα επεξεργαστούν φωτογραμμετρικά και θα αποδώσουν το τελικό προϊόν.Άλλωστε η μέθοδος αποτύπωσης που θα χρησιμοποιηθεί εξαρτάται τόσο από το τελικό παραδοτέο προϊόν, που θα προδιαγράψει και την ακρίβεια του σχεδιαγράμματος αποτύπωσης-ψηφιοποίησης όσο και από το κόστος της εφαρμοσμένης τεχνικής [97].
Πλεονεκτήματα – μειονεκτήματα και Χαρακτηριστικά
Κύρια χαρακτηριστικά της τοπογραφικής μεθόδου είναι:
- Η τοπογραφική αποτύπωση είναι αντικειμενική
- Ορίζει ένα σύστημα αναφοράς βάσει του οποίου γίνεται ο προσδιορισμός των μετρήσεων στο χώρο
- Η ανακατασκευή γεωμετριών στην αναπαράσταση γίνεται μέσω συγκεκριμένων σημείων, που προσδιορίζονται αυστηρά
- Υπάρχει δυνατότητα επιστημονικού ελέγχου του αποτελέσματος και ικανοποίηση των απαιτήσεων ακρίβειας και αξιοπιστίας.
- Υπάρχει δυνατότητα και έμμεσων μετρήσεων, ως παράγωγων των πρωτογενών άμεσων μετρήσεων.
- Λόγω της πεπερασμένης ικανότητας για ικανοποίηση συνθηκών πυκνότητας, υπάρχει δυσκολία παρακολούθησης της συνέχειας γεωμετρικών στοιχείων (π.χ., γραμμές και κυρίως επιφάνειες).
- Το μέγεθος της πυκνότητας, που επηρεάζει την πιστότητα της αναπαρά-στασης, συναρτάται από τον χρόνο παραμονής στο πεδίο.
- Είναι δυνατή η τοποθέτηση, στην αναπαράσταση, περισσότερων αντικειμένων σε αμοιβαία σχέση μεταξύ τους.
- Υπάρχει ανάγκη για στοιχειώδη σχεδιαστική ικανότητα στο πεδίου, για τη σύνταξη σκαριφημάτων, κλπ.)
- Αντιμετωπίζονται δύσκολα και μόνο μετά από κατάλληλη μαθηματική στατιστική επεξεργασία (στο γραφείο), περιπτώσεις μη-επιπεδότητας.
- Υπάρχει σημαντικό πρόβλημα χρόνου και κόστους εργασιών πεδίου, που εξαρτάται από την πολυπλοκότητα του αντικειμένου.
- Ο εξοπλισμός πεδίου είναι, κατ' αρχήν, μέτριου κόστους.
- Ο απαραίτητος εξοπλισμός για τις επεξεργασίες γραφείου είναι ο συνηθισμένος των τοπογραφικών εφαρμογών.
- Η αλγοριθμική επεξεργασία των δεδομένων είναι εύκολη.
- Δεν μπορούν να αντιμετωπιστούν λεπτομέρειες και πολύπλοκα αρχιτεκτονικά (κυρίως μη-γραμμικά) ή δύσκολα προσπελάσιμα στοιχεία του προς αποτύπωση αντικειμένου.
- Υπάρχει ανάγκη για πρόσθετες εργασίες, που χρησιμοποιούνται στην εμπειρική μέθοδο, όπως είναι π.χ. μετρήσεις με μετροταινία, ερασιτεχνικές φωτογραφίες κ.α.
- Η στερεομετρία του αντικειμένου ανακατασκευάζεται έμμεσα.
Εξοπλισμός
Για να γίνει εφικτή η μέτρηση των σημείων στο χώρο είναι απαραίτητο να χρησιμοποιηθούν ακριβή όργανα μετρήσεων. Το πλέον κοινό όργανο που χρησιμοποιείται στην τοπογραφία τόσο για την αποτύπωση μεσαίας αλλά και μικρής κλίμακας αντικειμένων είναι ο θεοδόλιχος ή ταχύμετρο. Ο θεοδόλιχος είναι σε θέση να μετρά με μεγάλη ακρίβεια την οριζόντια και κατακόρυφη γωνία που σχηματίζεται από τη νοητή οπτική γραμμή που συνδέει ένα χαρακτηριστικό σημείο του οργάνου (κέντρο σκόπευσης) και το σημείο λεπτομέρειας (σημείο σκόπευσης) επί του αντικειμένου που παρατηρείται μέσω του οπτικού συστήματος του. Έμμεσα με χρήση των εξισώσεων τριγωνομετρίας και της μέτρησης των κατακόρυφων γωνιών είναι εφικτό να μετρηθούν και οι κατακόρυφες αποστάσεις μεταξύ σημείων στον τρισδιάστατο χώρο. Με την επίλυση των θεμελιωδών θεωρημάτων της τοπογραφίας όλες οι μετρήσεις των γωνιών που γίνονται μέσω του θεοδόλιχου μπορούν να οδηγήσουν σε υπολογισμό των τρισδιάστατων συντεταγμένων των παρατηρούμενων σημείων στο επίγειο καρτεσιανό τρισορθογώνιο σύστημα συντεταγμένων.
Αν και οι θεοδόλιχοι αρχικά κατασκευάστηκαν μόνο για κάνουν μετρήσεις γωνιών, τα σύγχρονα όργανα συνοδεύονται από αποστασιόμετρα οπότε ονομάζονται Γεωδαιτικοί Σταθμοί (Total Station) και επιτρέπουν με μία μόνο σκόπευση (δηλαδή μέτρηση της οριζόντιας και κατακόρυφης γωνίας) και την ταυτόχρονη μέτρηση της απόστασης του σημείου λεπτομέρειας από το θεοδόλιχο να παράγουν τις απ’ ευθείας τρισδιάστατες συντεταγμένες σημείων στο χώρο εφόσον είναι απόλυτα προσδιορισμένη η θέση (ονομάζεται και στάση του οργάνου στην τοπογραφική ορολογία) του τοπογραφικού οργάνου σε ένα τρισορθογώνιο σύστημα συντεταγμένων.
Συγκεκριμένα για τη μέτρηση αποστάσεων μπορούν να χρησιμοποιηθούν οι τρεις παρακάτω τρόποι:
- Μηχανική μέθοδος. Γίνεται με τη χρήση ειδικών μεταλλικών μετροταινιών και συρμάτων invar.
- Οπτική μέθοδος. Γίνεται με την παρατήρηση μέσω του οπτικού συστήματος ενός οργάνου μιας ειδικής μετρητικής διάταξης.
- Ηλεκτρομαγνητική μέθοδος. Για την μέτρηση της απόστασης με χρήση του τοπογραφικού οργάνου απαιτείται συνήθως η εφαρμογή ενός ανακλαστήρα που εφάπτεται του σημείου που απαιτείται να μετρηθεί. Υπάρχουν οι εξής τρόποι για τον υπολογισμό της απόστασης:
- Παλμού. Βασίζεται στο χρόνο που απαιτείται για την μετάδοση ενός ηλεκτρομαγνητικού σήματος μεταξύ του οργάνου που φέρει και την πηγή του Η/Μ κύματος και του σημείου που επιθυμείται η μέτρηση της απόστασής του από αυτό.
- Σύγκρισης φάσεων. Ο πομπός του οργάνου παράγει ένα ημιτονοειδές μετρικό σήμα το οποίο αντανακλάται και επιστρέφει με διαφορετική φάση. Η διαφορά φάσης καταγράφεται και μετατρέπεται σε απόσταση.
- Τα τελευταία χρόνια η ανάπτυξη και εξέλιξη των αποστασιόμετρων laser και των οργάνων μέτρησης απόστασης με χρήση της τεχνολογίας των υπέρυθρων ακτίνων έδωσε τη δυνατότητα να
γίνονται οι μετρήσεις χωρίς να είναι απαραίτητη η χρήση
ανακλαστήρα (πρίσμα ή κάτοπτρο).
Βασική Τοπογραφική Ορολογία
Τα θεμελιώδη προβλήματα της τοπογραφίας μπορούν να οδηγήσουν στον υπολογισμό των τρισδιάστατων συντεταγμένων των σημείων που παρατηρήθηκαν μέσω του οπτικού συστήματος τους και καταγράφηκαν οι γωνίες προσανατολισμού τους σε σχέση με μια γνωστή διεύθυνση που συνήθως είναι ο γεωγραφικός βορράς.
Προτού οριστούν τα θεμελιώδη προβλήματα και η βασική μαθηματική επεξεργασία που οδηγεί στον προσδιορισμό των συντεταγμένων στο χώρο, εξηγούνται ορισμένοι όροι που θα συναντηθούν παρακάτω:
Μονάδα μέτρησης γωνιών grad: Η μονάδα μέτρησης των γωνιών σε προβλήματα τοπογραφίας είναι ο βαθμός (grad=1g) όπου ο πλήρης κύκλος αποτελείται από 400g και οι υποδιαιρέσεις του είναι το c και το cc. 1g αποτελείται από 100c και ένα 1c από 100cc. Η μεγάλη ακρίβεια και το ισχυρό πλεονέκτημα της Τοπογραφίας σε σχέσεις με τις υπόλοιπες μεθόδους μετρήσεων οφείλεται στην υψηλή ακρίβεια μετρήσεων των γωνιών με χρήση των τοπογραφικών οργάνων και μπορεί να αγγίζει τα μερικά cc.
Γωνία διεύθυνσης G: Η γωνία που λαμβάνεται με αφετηρία τη διεύθυνση του βορρά (που συμπίπτει συνήθως με τον θετικό ημιάξονα Y του συστήματος αναφοράς καρτεσιανών συντεταγμένων) και καταλήγει μέχρι τη διεύθυνση(i->j) που συνδέει δύο σημεία στο επίπεδο (Εικόνα 3). Η φορά διαγραφής της γωνίας διεύθυνσης είναι δεξιόστροφη δηλαδή σύμφωνα με την κίνηση των δεικτών του ρολογιού και παίρνει τιμές από 0o μέχρι 400g.
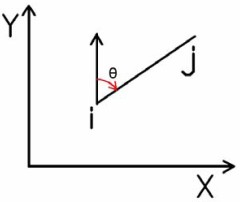
Εικόνα 3. Ορισμός της γωνίας διεύθυνσης
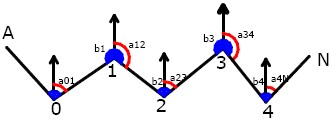
Εικόνα 4. Πολυγωνική όδευση
Πολυγωνική Όδευση: Η όδευση αποτελείται από μια σειρά διαδοχικώνσημείων που σχηματίζουν στην οριζόντια προβολής τους μια τεθλασμένηγραμμή (ανοικτή ή κλειστή). Η επίλυση της όδευσης οδηγεί στον προσδιορισμότων συντεταγμένων όλων των σημείων που την αποτελούν (κορυφών της οδευσης) σε ένα καρτεσιανό σύστημα αναφοράς που μπορεί να είναι το Εθνικό Γεωγραφικό Σύστημα Αναφοράς (ΕΓΣΑ) ή ένα ανεξάρτητο τοπικό σύστημα αναφοράς ανάλογα με τα σημεία εξάρτησης και προσανατολισμού. Η διαδικασία προσδιορισμού των συντεταγμένων των κορυφών της όδευσης ονομάζεται πολυγωνομετρία.
Είδη οδεύσεων: Ανάλογα με το είδος του πολυγώνου που σχηματίζουν οι τεθλασμένες γραμμές της όδευσης διακρίνονται οι οδεύσεις σε ανοικτές και κλειστές. Ανεξάρτητες ονομάζονται οι οδεύσεις που δεν συνδέονται οι συντεταγμένες των κορυφών τους με ένα τοπικό ή εθνικό γεωγραφικό σύστημααν αφοράς. Διαφορετικά, αν η θέση τουλάχιστον μιας κορυφής της όδευσης είναι δεδομένη σε ένα τοπικό εθνικό σύστημα γεωγραφικής αναφοράς ονομάζεται εξαρτημένη. Υπάρχει περίπτωση η όδευση να συνοδεύεται από μια εξάρτηση που αφορά στον προσανατολισμό οπότε η εξαρτημένη όδευση ονομάζεται προσανατολισμένη κατά το ένα ή κατά τα δύο άκρα της.
Γωνίες θλάσεως: Είναι οι γωνίες μεταξύ των πλευρών της όδευσης πουβρίσκονται στα αριστερά κατά την πορεία επίλυσης.
Βασική επεξεργασία – Θεμελιώδη προβλήματα τοπογραφίας
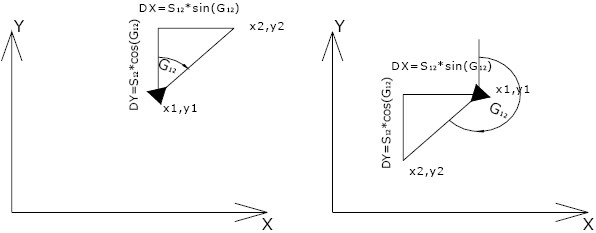
Εικόνα 5. Πρώτο θεμελιώδες πρόβλημα
Το πρώτο θεμελιώδες πρόβλημα της τοπογραφίας οδηγεί σε υπολογισμό των οριζοντιογραφικών συντεταγμένων ενός σημείου όταν είναι γνωστά ταπαρακάτω
- Οι οριζοντιογραφικές (ή επίπεδες) συντεταγμένες (x1,y1) ενός σημείου
- H γωνία διεύθυνσης G12 από το σημείο 1 προς το σημείο 2
- Η οριζόντια απόσταση (S12) ανάμεσα στα δύο σημεία.
Η εφαρμογή του πρώτου θεμελιώδους προβλήματος γίνεται όταν μετά από την επίλυση της όδευσης είναι γνωστές οι συντεταγμένες των κορυφών της όδευσης.
Αν ο θεοδόλιχος έχει τοποθετηθεί στη θέση με οριζοντιογραφικές συντεταγμένες (x1,y1) ο υπολογισμός των συντεταγμένων (x2,y2) του σημείου που παρατηρείται από το οπτικό σύστημα του οργάνου μπορεί να υπολογιστεί σύμφωνα με τις παρακάτω εξισώσεις:
Χ2=Χ1+Dx=Χ1+S12*sin(G12) (1)
Υ2=Υ1+Dy=Υ1+S12*cos(G12)
όπου G12 είναι η γωνία που θα διαγράψει ο άξονας των Y (βορράς) αν κινηθεί σύμφωνα με τη φορά των δεικτών του ρολογιού ώστε να συμπέσει με τη νοητή γραμμή που συνδέει τα δυο σημεία και S12 η οριζόντια απόσταση ανάμεσα στο σημείο στάσης του οργάνου και το σημείο σκόπευσης (x2,y2).
Το αντίστροφο ή δεύτερο θεμελιώδες πρόβλημα της τοπογραφίας μπορεί να οδηγήσει σε υπολογισμό της απόστασης (S12) δύο σημείων και της γωνίας διεύθυνσης (G12) που σχηματίζει η νοητή ευθεία που τα ενώνει με το θετικό ημιάξονα των τεταγμένων, εφόσον είναι γνωστές οι συντεταγμένες τουσημείου.
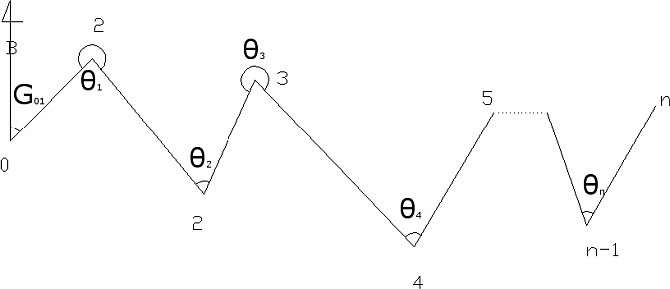
Εικόνα 6. Τρίτο θεμελιώδες πρόβλημα ή μεταφορά γωνίας διεύθυνσης
Το τρίτο θεμελιώδες πρόβλημα της τοπογραφίας (μεταφορά γωνίας διεύθυνσης) (Εικόνα 6) οδηγεί στον προσδιορισμό της γωνίας διεύθυνσης μιας οποιασδήποτε πλευράς της τεθλασμένης γραμμής (ή πολυγωνικής όδευσης) Gn(n+1) όταν είναι γνωστές οι προηγούμενες γωνίες θλάσεις και η γωνία διεύθυνσης της πρώτης πλευράς.
Η σχέση που δίνει τη γωνία διεύθυνσης είναι:
Gn(n+1)=G(n-1)n+θ1+200g (2)
Εφαρμόζοντας τη σχέση για όλες τις μετρήσεις των γωνιών μιας όδευσης προκύπτει τελικά η σχέση που αποδίδει τη γωνία διεύθυνσης μιας πλευράς
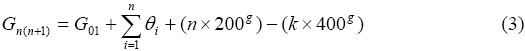
όταν είναι γνωστές οι γωνίες θλάσεις των προηγούμενων πλευρών και η γωνία διεύθυνσης της πρώτης πλευράς.
Οπισθοτομία: Η διαδικασία υπολογισμού των συντεταγμένων του σημείου στάσης του οργάνου μετά από μέτρηση των διευθύνσεων προς τρία τουλάχιστον γνωστά σημεία Α,Β,Γ. Υπάρχουν τρεις μέθοδοι για τον υπολογισμό των συντεταγμένων της στάσης του οργάνου με οπισθοτομία οι Βαρυκεντρική, Collins και Τομής δύο κύκλων, ωστόσο για λόγους συντομίας περιγράφεται η πιο κοινή (Βαρυκεντρική).
Βαρυκεντρική (Tienstra) μέθοδος οπισθοτομίας: Η στάση που τοποθετείται το τοπογραφικό όργανο (οπισθοτομικό σημείο) πρέπει να εντοπίζεται κατά προτίμηση στο κέντρο βάρους των γνωστών σημείων και σε κάθε περίπτωση εντός του τριγώνου. Μετρούνται οι διευθύνσεις προς τρία γνωστά σημεία από τις οποίες προκύπτουν οι γωνίες γ1,γ2,γ3 (Εικόνα 7) και οι σχέσεις που δίνουν τις οριζόντιες συντεταγμένες του σημείου Ρ είναι:
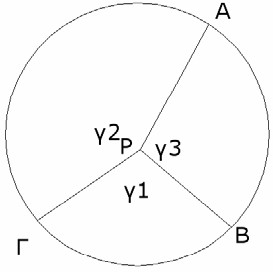
Εικόνα 7. Βαρυκεντρική μέθοδος οπισθοτομίας
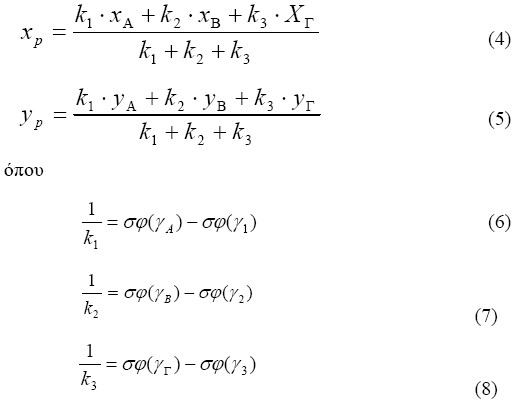
Οι γωνίες γΑ, γΒ και γΓ προκύπτουν από το δεύτερο και τρίτο θεμελιώδες πρόβλημα με γνωστές τις συντεταγμένες των σημείων. Το αλγεβρικό άθροισμα των γωνιών γ1,γ2 και γ3 είναι 400g.
Εμπροσθοτομία: Είναι η μέθοδος προσδιορισμού των συντεταγμένων ενός σημείου με μετρήσεις μόνο των γωνιών από άλλα δύο σημεία (τις στάσεις του οργάνου). Υπάρχουν τρεις μέθοδοι επίλυσης της εμπροσθοτομίας (επίλυση τριγώνου και θεμελιώδη προβλήματα, με μετρημένες γωνίες και με γωνίες διεύθυνσης). Ωστόσο για λόγους συντομίας περιγράφονται η πρώτη και δεύτερη μέθοδοι που είναι η πιο κοινές.
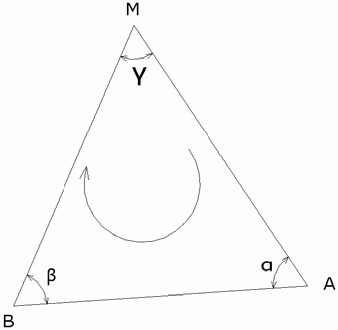
Εικόνα 8. Εφαρμογή εμπροσθοτομίας
Μέθοδος εμπροσθοτομίας με επίλυση τριγώνου και θεμελιώδη προβλήματα:
Τα σημεία Α,Β έχουν γνωστές συντεταγμένες ΧA,ΥA και ΧB,ΥB και μεεφαρμογή του πρώτου θεμελιώδους προβλήματος υπολογίζονται η απόστασηSAB και η γωνία διεύθυνσης GAB. Σύμφωνα με το νόμο των ημίτονων οιαποστάσεις SAM και SBM προκύπτουν από τις σχέσεις
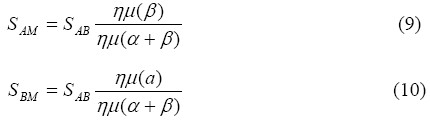
Με εφαρμογή του 3ου θεμελιώδους προβλήματος της τοπογραφίας υπολογίζονται οι γωνίες διευθύνσεις GAM και GBM
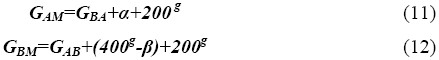
Με γνωστά τα ΧΑ,ΥΑ και GAM και SAM υπολογίζονται οι συντεταγμένες του σημείου Μ (XM,YM) από το 1ο θεμελιώδες πρόβλημα:

Για έλεγχο και μόνο υπολογίζονται οι συντεταγμένες του σημείου Μ (XM,YM) και από το σημείο Β:

Μέθοδος εμπροσθοτομίας με μετρημένες γωνίες: Απ΄ ευθείας από τις σχέσεις (χωρίς επίλυση του τριγώνου) έχουμε:
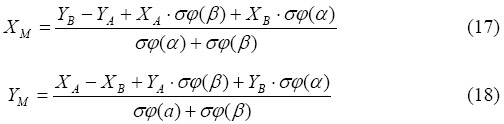
Με χρήση των προηγούμενων προβλημάτων ή της μεθόδου οπισθοτομίας μπορεί να δημιουργηθεί ένα δίκτυο μετρημένων σημείων γύρω από το χώρο ή το κτίριο μελέτης και στη συνέχεια με χρήση μεθόδων εμπροσθοτομίας ή του πρώτου θεμελιώδους προβλήματος να υπολογιστούν οι συντεταγμένες όλων των σημείων που παρατηρούνται από το σύστημα σκόπευσης του οργάνου (γεωδαιτικού σταθμού).
Υπολογισμός υψομέτρων των παρατηρούμενων σημείων
Οι τοπογραφικές μέθοδοι που παρουσιάστηκαν αφορούσαν τον υπολογισμό της οριζοντιογραφικής θέσης των σημείων στο χώρο. Ο προσδιορισμός της τρίτης διάστασης, που συμπίπτει με το υψόμετρο, κάθε χαρακτηριστικού σημείου στο χώρο μπορεί να γίνει χρήση της μεθόδου της Τριγωνομετρικής Υψομετρίας ή με την εφαρμογή της Γεωμετρικής Χωροστάθμησης εφόσον βέβαια υπάρχουν μετρήσεις από ένα άλλο τοπογραφικό όργανο το χωροβάτη.
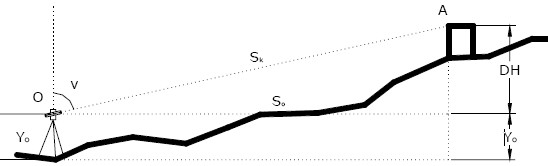
Εικόνα 9. Τριγωνομετρική υψομετρία
Θα αναφερθούμε για λόγους συντομίας στον υπολογισμό των υψομέτρων με την πρώτη μέθοδο.
Η Τριγωνομετρική Υψομετρία εκμεταλλεύεται τη μέτρηση των κατακόρυφων γωνιών που μετρώνται από ένα γεωδαιτικό σταθμό και της κεκλιμένης απόστασης του οργάνου από το σημείο που θέλουμε να υπολογιστεί το υψόμετρό του. Εξετάζοντας το σχήμα και εφαρμόζοντας το πυθαγόρειο θεώρημα εύκολα προκύπτει η σχέση που δίνει την υψομετρική διαφορά ανάμεσαστο κέντρο σκόπευσης Ο του γεωδαιτικού σταθμού και το σημείο Α:
ΔΗΟΑ=Sκ συν(v) (19)
όπου Sκ είναι η κεκλιμένη απόσταση του οργάνου από το σημείο, v η κατακόρυφη γωνία που σχηματίζει το ζενίθ με την οπτική γραμμή που συνδέει το όργανο με το σημείο Α.
Το τελικό αποτέλεσμα που θα δώσει και την συντεταγμένη Ζ του σημείου Α πρέπει να προστεθεί το ύψος τοποθέτησης του οργάνου Υο και το υψόμετρο του σημείου στο έδαφος που έχει προκύψει από προηγούμενη Τριγωνομετρική Υψομετρία ή Γεωμετρική Χωροστάθμηση.
Σε περίπτωση που δεν μπορεί να μετρηθεί η κεκλιμένη απόσταση του κέντρου σκόπευσης του οργάνου από το σημείο Α αλλά αν είναι γνωστή η οριζόντια απόσταση Sο του οργάνου από το σημείο η σχέση που δίνει τηδιαφορά ΔΗΟΑ είναι:
ΔΗΟΑ=Sο σφ(v) (20)


