Τα γεωμετρικά χαρακτηριστικά των τρίγωνων αποτελούν την βάση για πολλές τεχνικές μετρήσεων. Από τις βασικές μετρήσεις γεωδαισίας που πραγματοποιούνταν στην αρχαία Ελλάδα μέχρι και σήμερα με τους τρισδιάστατους σαρωτές λέιζερ, η χρήση των τριγώνων είναι θεμελιώδης. Ο Θαλής (6ος π.χ. αιώνας) διακρίθηκε για την διατύπωση πέντε γεωμετρικών θεωρημάτων, το βασικότερο εκ των οποίων είναι ο νόμος των συνημίτονων που μας παρέχει άμεση λύση στο πρόβλημα της τριγωνοποίησης.
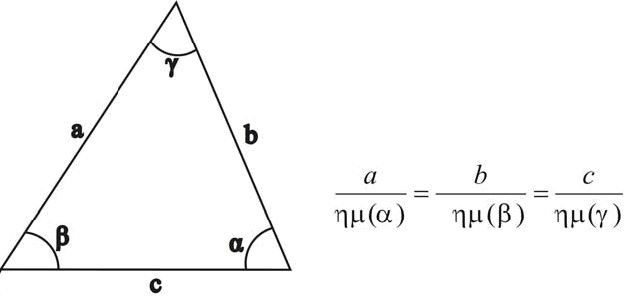
Εικόνα 8: Νόμος ημιτόνων
Οι πηγές ακτίνων λέιζερ έχουν μεγάλη εφαρμογή στην τρισδιάστατη σάρωση λόγω των ιδιαίτερων χαρακτηριστικών της ακτινοβολίας που εκπέμπουν. Τα κυριότερα χαρακτηριστικά μιας δέσμης φωτός λέιζερ είναι η μικρή της διασπορά-απόκλιση, η μεγάλη και συγκεντρωμένη ισχύ της, που διατηρείται σε μεγάλες αποστάσεις και η εκπομπή της σε συγκεκριμένο μήκος κύματος, δηλαδή είναι μονοχρωματική. Οι ιδιότητες αυτές των ακτίνων laser τις καθιστούν την ιδανικότερη επιλογή για κατάδειξη χωρίς φυσική επαφή. Τα συστήματα που βασίζονται στην εκπομπή ακτίνων λέιζερ χρησιμοποιούν διαφορετικά μοτίβα φωτός. Στην παρακάτω εικόνα (εικόνα 9) παρουσιάζονται κάποια από τα πλέον κλασικά μοτίβα προβολής που απαντώνται σε εμπορικά αλλά και ερευνητικά συστήματα.

Εικόνα 9: δομημένα προβαλλόμενα μοτίβα για 3D σάρωση
Οι σαρωτές αντικειμένων που βασίζονται σε ακτίνες λέιζερ χρησιμοποιούνται κυρίως σε αποστάσεις μικρότερες των δέκα μέτρων και θα μπορούσαμε να τους κατατάξουμε σε κατηγορίες ανάλογα με το πλήθος οπτικών αισθητήρων που χρησιμοποιούν. Έτσι σε σαρωτές με έναν αισθητήρα εικόνας υπάρχει μια πηγή που προβάλει την ακτίνα λέιζερ σε μια συγκεκριμένη και μεταβαλλόμενη προς την επιφάνεια του αντικείμενου γωνία. Ένας αισθητήρας εικόνας CCD ή CMOS βρίσκεται στην άλλη άκρη της βάσης του συστήματος και αναλαμβάνει τον εντοπισμό του σημείου ή της περιοχής που περιγράφει η ακτίνα λέιζερ καθώς ανακλάται στην επιφάνεια του αντικειμένου. Η προβολή της ακτίνας μπορεί να σχηματίζει απλά ένα φωτεινό σημείο, μια γραμμή, ένα μοτίβο από ρίγες ή ακόμα και ένα στατικό τυχαίο πλέγμα (Εικόνα 9). Η τρισδιάστατη θέση της επιφάνειας του αντικειμένου που αντανακλά την ακτίνα μπορεί να βρεθεί από το ιδεατό τρίγωνο που δημιουργείται. Η ακρίβεια μέτρησης βάθους μειώνεται ανάλογα με την απόσταση ανάμεσα στο σαρωτή και το αντικείμενο. Για πρακτικούς λόγους, η απόσταση ανάμεσα στους οπτικούς αισθητήρες και στην πηγή της ακτίνας λέιζερ δεν μπορεί να μεταβάλλεται ανάλογα.
Η χρήση δύο οπτικών αισθητήρων αποτελεί μια παραλλαγή της αρχικής ιδέας τριγωνοποίησης. Οι αισθητήρες βρίσκονται στα δύο άκρα της βάσης του σαρωτή. Το σημείο αντανάκλασης της ακτίνας λέιζερ γίνεται αντιληπτό και από τους δύο αισθητήρες. Η γεωμετρική λύση είναι ίδια με αυτήν του ενός αισθητήρα άρα και τα αποτελέσματα έχουν την ίδια ακρίβεια. Ο δεύτερος αισθητήρας χρησιμοποιείται για την γρηγορότερη σάρωση αφού η πολυμορφία της επιφάνειας των αντικειμένων προκαλεί συχνά την αδυναμία του ενός αισθητήρα να φτάσει σε κάποια σημεία που την ίδια στιγμή μπορεί να είναι εμφανή στο δεύτερο αισθητήρα λόγω της διαφορετικής του θέσης και γωνίας.
Η οπτική τριγωνοποίηση είναι μια τεχνική που εφαρμόζεται για περισσότερο από είκοσι χρόνια για την μέτρηση αποστάσεων. Τα τελευταία χρόνια όμως η ανάπτυξη γεωμετρικά σταθερών αισθητήρων και διόδων φωτός βελτίωσε κατά πολύ την ακρίβεια και την ταχύτητα της εν λόγω τεχνικής. Η ποικιλία στους σαρωτές τριγωνοποίησης βασίζεται κυρίως στη
- δομή του φωτισμού (απλό σημείο, ακτίνα λέιζερ, πολλαπλός πίνακας σημείων ή πολλαπλές δέσμες ακτίνων),
- μορφή του αισθητήρα (γραμμικός πίνακας ή πλέγμα CCD ή CMOS)
- μέθοδο σάρωσης (μετακίνηση του αντικειμένου μπροστά από την πηγή φωτός ή μετακίνηση του ίδιου του συστήματος γύρω από το αντικείμενο).
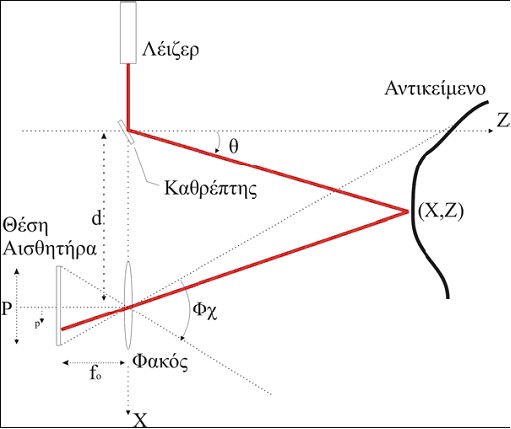
Στην Εικόνα 10 επεξηγείται το πρόβλημα της τριγωνοποίησης σε δύο διαστάσεις. Η θέση του κέντρου του παλμού της δέσμης φωτός που αντανακλάται στην επιφάνεια αποτυπώνεται πάνω στον αισθητήρα εικόνας. Ο σαρωτής με την σειρά του υπολογίζει τη νοητή γραμμή που τέμνει τη δέσμη σε ένα ακριβώς σημείο και αυτό έχει ως αποτέλεσμα την ανάκτηση του βάθους. Το τρισδιάστατο σχήμα του αντικειμένου προκύπτει από την μετακίνηση και περιστροφή του αντικείμενου μπροστά από την σταθερή ακτίνα που προβάλει ο σαρωτής.Υπάρχει όμως και η παραλλαγή της μεθόδου όπου η σάρωση του αντικείμένου πραγματοποιείται με την ακτίνα λέιζερ να μετακινείται γύρω από το αντικείμενο. Η ακρίβεια της οπτικής τριγωνοποίησης βασίζεται στην ικανότητα εντοπισμού του κέντρου του παλμού της δέσμης σε κάθε χρονική στιγμή.
Σε συστήματα οπτικής τριγωνοποίησης κοντινών αποστάσεων, όπου το βάθος υπολογίζεται από έναν και μόνο παλμό φωτός, παράγεται ένα καθορισμένο εύρος σφαλμάτων. Τα σφάλματα αυτά εμφανίζονται λόγω της αντανάκλασης της δέσμης στην επιφάνεια του αντικειμένου αλλά και εξαιτίας των χαρακτηριστικών της ίδιας της επιφάνειας [
3].
Εικόνα 10
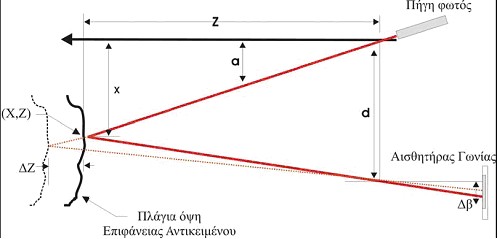
Η βασική γεωμετρική αρχή των συστημάτων τριγωνοποίησης περιγράφεται στο Εικόνα 10. Μπορείτε να διακρίνετε το συσχετισμό ανάμεσα στο σχήμα αυτό και στο σχήμα που περιγράφει τον νόμο των συνημίτονων (Εικόνα 8). Γνωρίζοντας τις δύο γωνίες (α και Δβ) ενός τριγώνου που είναι πάντα σχετικές με τη βάση του (d) τότε όλα τα χαρακτηριστικά και οι διαστάσεις του τριγώνου μπορούν να οριστούν πλήρως. Σε κάθε αλλαγή της απόστασης ΔΖ, μπορεί να υπολογιστεί η γωνία Δβ με το θεώρημα των αντίθετων γωνιών, θεωρώντας ότι το α είναι πάντα σταθερό. Ο αισθητήρας γωνίας είναι σταθερός. Για τον υπολογισμό της θέσης της επιφάνειας του αντικειμένου απαιτείται η σάρωση της κάθε δισδιάστατης εικόνας που αποτυπώνει ο οπτικός αισθητήρας, ώστε να βρεθεί το σημείο με την μέγιστη συγκέντρωση φωτός. Η διάταξη που παρουσιάζει το Εικόνα 10 είναι γνωστή ως σύστημα μονού σημείου ακτίνας λέιζερ. Στην Εικόνα 11 η ακτίνα φωτός αντανακλάται από έναν καθρέφτη και προβάλλεται στη συνέχεια μέσω αυτού πάνω στην επιφάνεια του αντικείμενου. Το οπτικό σύστημα αποτελείται από ένα φακό και ένα αισθητήριο το οποίο αποτυπώνει ψηφιακά την θέση της δέσμης φωτός πάνω στο αντικείμενο. Με απλή τριγωνομετρία, οι συντεταγμένες (x, z) του φωτιζόμενου σημείου μπορούν να υπολογιστούν. Οι υπολογισμοί γίνονται με τους εξής μαθηματικούς τύπους:
όπου p είναι η θέση του σημείου του αντικειμένου, όπως παρουσιάζεται πάνω στον αισθητήρα, θ είναι η γωνία απόκλισης της ακτίνας λέιζερ, ενώ d είναι η απόσταση ανάμεσα στον φακό και την πηγή της ακτίνας. fo είναι η απόσταση ανάμεσα στον αισθητήρα και το φακό. Οι περιορισμοί της μεθόδου τριγωνοποίησης μπορούν να αποδειχθούν αν προσπαθήσουμε να υπολογίσουμε την απόκλιση σφάλματος στον άξονα z, ορίζοντας το σz ως μια συνάρτηση του p. Ο νόμος διάδοσης των σφαλμάτων είναι:
όπου σρ είναι η τυπική απόκλιση σφαλμάτων για κάθε μέτρηση του σημείου p. Ως εκ τούτου, η τυπική απόκλιση εκφράζει την απροσδιοριστία του z που είναι αντιστρόφως ανάλογη με την βάση της κάμερας και την εστιακή απόσταση του φακού. Το μέγεθος της παραμέτρου d περιορίζεται κυρίως από:
- τα κατασκευαστικά στοιχεία των οπτικών τμημάτων του συστήματος (η σταθερότητα του όλου συστήματος μειώνεται όσο το d αυξάνεται)
- τις σκιές που δημιουργούνται (προβλήματα αυτό-απόφραξης με την αύξηση του d)
- Το πεδίο όρασης Φχ δίνεται από τον τύπο
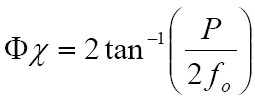 όπου P είναι το μήκος της απόστασης θέσης του αισθητήρα.
όπου P είναι το μήκος της απόστασης θέσης του αισθητήρα.
Συνεπώς, σε μια τυπική κατασκευή ενός συστήματος σάρωσης υπάρχει ένας συμβιβασμός ανάμεσα στην εστιακή απόσταση, στην απροσδιοριστία μέτρησης της τρίτης διάστασης και των σκιών που μπορεί να δημιουργηθούν. Ένας τρισδιάστατος σαρωτής που βασίζεται στην τριγωνοποίηση εμφανίζει συνήθως μια τυπική απόκλιση (σz) της τάξης των 50 – 150 μm. Ο Rioux [
1] παρουσίασε μια καινοτόμο προσέγγιση στην σάρωση με τριγωνοποίηση. Προτείνει ένα συγχρονισμένο σύστημα που μπορεί να σαρώσει σε πολύ μεγάλες εστιακές αποστάσεις με πολύ μικρές γωνίες τριγωνοποίησης χωρίς να τίθεται θέμα συμβιβασμού στην ακρίβεια των αποτελεσμάτων. Με μικρές γωνίες τριγωνοποίησης επιτυγχάνεται, επίσης, μείωση στην εμφάνιση πιθανών σκιών. Ο απώτερος σκοπός δεν είναι άλλος από τον συγχρονισμό της προβολής της ακτίνας λέιζερ και του εντοπισμού της. Όπως περιγράφεται στην Εικόνα 12, το οπτικό πεδίο του ανιχνευτή θέσης ακολουθεί το σημείο καθώς σαρώνει τη σκηνή. Η εστιακή απόσταση του φακού σχετίζεται με το επιθυμητό βάθος πεδίου, ή την περιοχή μέτρησης και όχι με το οπτικό πεδίο. Η ανάπτυξη σαρωτών αυτόματου συγχρονισμού έχει αποφέρει σημαντικές μειώσεις στις διαστάσεις της οπτικής κεφαλής των συστημάτων.
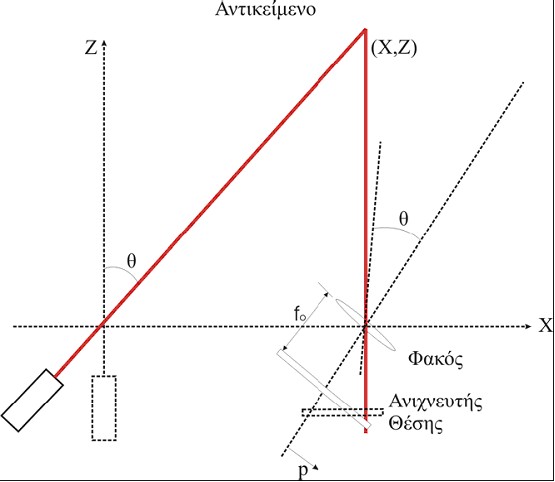
Εικόνα 12
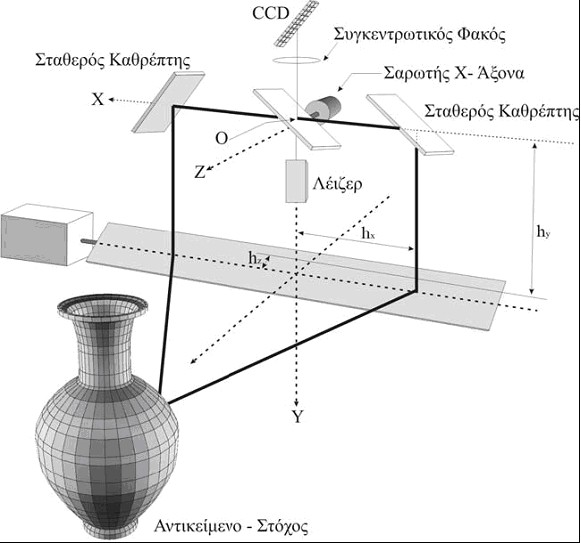
Όπως προαναφέρθηκε, για μια πλήρη τρισδιάστατη αποτύπωση ενός αντικειμένου απαιτείται είτε η μετακίνηση του σαρωτή γύρω από το αντικείμενο είτε κάποια άλλη μέθοδος. Η μηχανική μετατόπιση βασισμένη σε γαλβανόμετρα είναι μια μέθοδος που επιτρέπει τη μετατόπιση της δέσμης φωτός πάνω σε επιφάνειες. Η βασική οργάνωση των οπτικών τμημάτων ενός τέτοιου συστήματος περιγράφεται στην Εικόνα 13. Οι καθρέφτες περιστρέφονται γύρω από το κέντρο ενός νοητού άξονα με τη χρήση γαλβανόμετρων. Ο άξονας Χ (μεγάλη ταχύτητα σάρωσης) χρησιμοποιείται για τη γραμμική σάρωση, ενώ ο άξονας Υ (μικρή ταχύτητα σάρωσης) ανακλά κάθετα την ακτίνα, ώστε να δημιουργήσει την εικόνα που καταγράφεται από ένα CCD.
Εικόνα 13
Το τρισδιάστατο μοντέλο της επιφάνειας του αντικειμένου προκύπτει από μια ακολουθία διαδικασιών. Αυτές είναι οι εξής:
- εκπομπή της δέσμης φωτός (ακτίνα λέιζερ)
- συλλογή της δέσμης καθώς διασκορπίζεται στην σκηνή (μαζί με όλες τις μεταβολές που δέχεται εξαιτίας της ανάκλασης πάνω στις επιφάνειες του αντικειμένου) σε συγχρονισμό με τους καθρέφτες προβολής.
- συγκέντρωση της δέσμης στο γραμμικό ανιχνευτή θέσης γνωστό και ως CCD.
Πιο συγκεκριμένα, από τη διαδικασία πρόσκτησης των εικόνων εξάγονται τρεις διαφορετικές πληροφορίες σε κάθε βήμα της διαδικασίας δειγματοληψίας:
- δύο γωνιακές θέσεις των καθρεφτών και
- θέση του στίγματος της ακτίνας λέιζερ πάνω στον ανιχνευτή θέσης
Οι εξισώσεις που παράγονται από την βαθμονόμηση του συστήματος χρησιμοποιούνται για την χαρτογράφηση των γωνιακών θέσεων και του στίγματος της ακτίνας φωτός πάνω σε ένα κλασικό καρτεσιανό σύστημα συντεταγμένων (x,y,z)[
5].
Σε πολλές εφαρμογές αποτύπωσης αντικειμένων πολιτισμικής κληρονομιάς, εκτός από τη γεωμετρία, η απόκτηση πληροφορίας υφής είναι απαραίτητη, καθώς προσφέρει μεγάλο ρεαλισμό, ιδιαίτερα όταν τα αντικείμενα φέρουν κάποιας μορφής διακόσμηση. Με την χαρτογράφηση της πληροφορίας υφής πάνω στην γεωμετρία επιτυγχάνεται μια φωτορεαλιστική απόδοση του αντικειμένου. Μερικοί σαρωτές μπορούν και καταγράφουν την ένταση του επιστρεφόμενου σήματος προς τον οπτικό αισθητήρα. Αυτή η πληροφορία, όμως, δεν είναι αρκετή για την ρεαλιστική απόδοση της υφής. Οι περισσότεροι εμπορικοί σαρωτές τριγωνοποίησης έχουν βελτιστοποιηθεί για την αναγνώριση της ακτίνας λέιζερ και του σημείου που καταδεικνύει και όχι για την αποτύπωση της πληροφορία υφής στο συγκεκριμένο σημείο. Υπάρχουν χρήστες που απαιτούν την ύπαρξη υψηλής ποιότητας φωτογραφικών μηχανών μέσα στο ίδιο σύστημα σάρωσης. Η λύση αυτή είναι όμως δαπανηρή και κάποιοι εκ των χρηστών δεν είναι έτοιμοι να ανταποκριθούν στο κόστος μιας τέτοιας επιπρόσθετης λειτουργίας. Μια τυπική λύση στο συγκεκριμένο πρόβλημα, που ακολουθείται από αρκετές εταιρείες, είναι η τοποθέτηση εξωτερικής ψηφιακής φωτογραφικής μηχανής πάνω στο σαρωτή με χρήση κάποιου συστήματος στήριξης και προσαρμογής. Σε τέτοιες περιπτώσεις είναι απαραίτητη η γνώση της σχετικής απόστασης σαρωτή και ψηφιακής φωτογραφικής μηχανής που χρησιμοποιείται για την βαθμονόμηση τους. Η βαθμονόμηση και των δύο θα επιτρέψει την χαρτογράφηση (UV mapping) των δυσδιάστατων εικόνων πάνω στην επιφάνεια του πολυγωνικού πλέγματος ή του νέφους σημείων.
Οι προδιαγραφές των εμπορικών σαρωτών, όπως δίνονται από τις κατασκευάστριες εταιρείες, πρέπει πάντα να τίθενται υπό αμφισβήτηση [
6]. Οι πιθανές αποστάσεις κάλυψης σχετίζονται με την ανακλαστικότητα του ίδιου του αντικειμένου αλλά και την διαύγεια της ατμόσφαιρας, την οποιαδήποτε άλλη επιπρόσθετη ακτινοβολία που μπορεί να προκαλείται από τεχνητή ακτινοβολία και άλλες πηγές παρεμβολής.
Η διαδικασία της βαθμονόμησης
Η διαδικασία βαθμονόμησης του ψηφιακού οπτικού συστήματος που χρησιμοποιεί ένας σαρωτής λέιζερ κοντινών αποστάσεων είναι βασικός παράγοντας της ορθής λειτουργίας του. Η διαδικασία βαθμονόμησης είναι συνήθως τυποποιημένη και περιλαμβάνει την αναγνώριση των εσωτερικών και εξωτερικών χαρακτηριστικών του οπτικού συστήματος με την βοήθεια ενός πραγματικού αντικείμενου που τα γεωμετρικά του χαρακτηριστικά είναι γνωστά με πολύ μεγάλη ακρίβεια. Τα χαρακτηριστικά αυτά βοηθούν στην εύρεση εκείνου του μαθηματικού μοντέλου που περιγράφει την εστιακή απόσταση, τις παραμορφώσεις που εισάγει ο φακός στην εικόνα, καθώς και άλλες παραμέτρους που έχουν εφαρμογή στη σάρωσης. Μετά τη σάρωση του γνωστού αντικειμένου η ακρίβεια και οι ανοχές μέτρησης του συστήματος μπορούν να υπολογιστούν. Αυτή η διαδικασία αποτελεί και τη φάση επαλήθευσης και επιβεβαίωσης των αποτελεσμάτων. Η ακρίβεια του συστήματος μπορεί να υπολογισθεί μέσω του γνωστού αντικειμένου βαθμονόμησης το οποίο αποτυπώνεται από διαφορετικές θέσεις και προσανατολισμούς. Ένας γενικός κανόνας που ακολουθείται στη συγκεκριμένη διαδικασία είναι πως τα χαρακτηριστικά του αντικειμένου βαθμονόμησης πρέπει να είναι γνωστά με ακρίβεια δέκα φορές μεγαλύτερη από αυτή που αποτυπώνει το ψηφιακό οπτικό σύστημα του σαρωτή.
Ανάλυση του σαρωτή
Η τελική ανάλυση ενός αντικειμένου είναι θεωρητικά μια συνάρτηση του μεγέθους των γωνιακών μεταβολών που μπορεί να αντιληφθεί το σύστημα καθώς η ακτίνα λέιζερ μετακινείται πάνω στις επιφάνειες. Μια πιο πρακτικής αξίας επεξήγηση της ανάλυσης σχετίζεται με το μέγεθος του στίγματος της ακτίνας λέιζερ που αντανακλάται. Αν η υψηλή ανάλυση είναι βασική προϋπόθεση σε μια εφαρμογή ψηφιοποίησης, τότε θα πρέπει με μεγάλη προσοχή να ελεγχθεί η βέλτιστη ικανότητα εστίασης της ακτίνας πάνω στο αντικείμενο είτε χειροκίνητα είτε μέσω κάποιας αυτοματοποιημένης διαδικασίας που φέρει ο σαρωτής, έτσι, ώστε η αποτύπωση της γεωμετρίας του αντικειμένου να γίνει με την υψηλότερη δυνατή ανάλυση. Στην Εικόνα 14 παρουσιάζεται στιγμιότυπο από διαδικασία ψηφιοποίησης στο επάνω τμήμα μιας προτομής. Η ρύθμιση της εστίασης γίνεται χειροκίνητα. Εμφανέστατη είναι η διαφορά έντασης της δέσμης καθώς ο σαρωτής πλησιάζει προς το σημείο βέλτιστης εστίασης.

Εικόνα 14
Η ανάλυση της οπτικής τριγωνοποίησης περιορίζεται από την περίθλαση της ακτίνας. Ακόμα και σε βέλτιστες περιπτώσεις εκπομπής, η δέσμη φωτός δεν διατηρεί τον απόλυτη ευθυγράμμιση με τον στόχο της. Στην πραγματικότητα, όσο μικρότερη είναι η ακτίνα λέιζερ τόσο μεγαλύτερη είναι η απόκλιση που δημιουργείται εξαιτίας της περίθλασης. Η περίθλαση της δέσμης επιβάλλει έναν περιορισμό στην ισχύ της ακτίνας λέιζερ. Το γράφημα στην Εικόνα 15 περιγράφει το βαθμό διάθλασης της ακτίνας καθώς μεταβάλλεται το μέγεθος των αντικειμένων. Ο διαχωρισμός των αντικειμένων έγινε με βάση τις διαστάσεις τους σε τρεις βασικές κατηγορίες. Ο περιορισμός αυτός έχει να κάνει με τα όρια ανάκτησης της δέσμης από τους αισθητήρες καθώς η δέσμη κινείται κατά μήκος των αξόνων x και y. Στην περίπτωση του άξονα z θα περίμενε κανείς μια συνεχόμενη βελτίωση καθώς η ισχύς της ακτίνας αυξάνεται και πλησιάζει την επιφάνεια του αντικειμένου. Δυστυχώς όμως κάτι τέτοιο δεν ισχύει. Μια λεπτομερής ανάλυση για τα χαρακτηριστικά της διάδοσης της δέσμης φωτός μπορεί να βρεθεί στην εργασία των Beraldin et al. [
5].
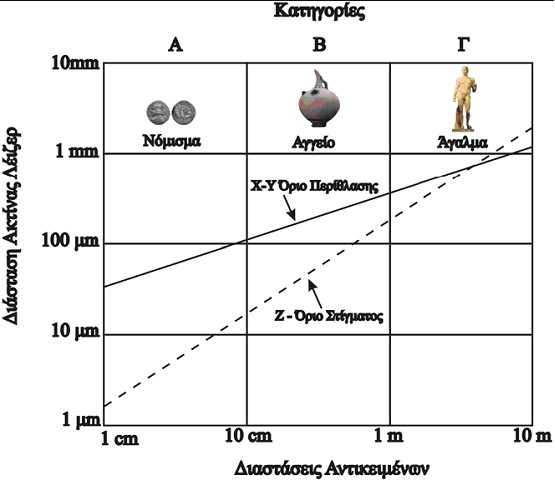
Εικόνα 15
Κοινό χαρακτηριστικό των σαρωτών κοντινών αποστάσεων αποτελεί το γεγονός ότι μεμονωμένα χαρακτηριστικά των αντικειμένων δεν μπορούν να αναγνωριστούν άμεσα. Οι μετρήσεις των αποστάσεων βάθους πολλές φορές αποκτούνται με βάση ένα τυπικό νοητό πλέγμα (π.χ. πλέγμα αισθητήρα CCD), το οποίο δεν μπορεί να εξασφαλίσει ότι κάθε δοθέν σημείο πάνω στο αντικείμενο συμπίπτει με ένα και μόνο ένα συγκεκριμένο σημείο πάνω στο πλέγμα. Οι μετρήσεις σημείο-προς-σημείο βασίζονται σε μεγάλο βαθμό σε παρεμβολή (interpolation). Αυτός ο περιορισμός είναι αποτέλεσμα της προκαθορισμένης χωρικής ανάλυσης του αισθητήρα εικόνας. Σε άλλες περιπτώσεις, όπως θα δούμε και παρακάτω (Σχήμα-Από-Δομημένο-Φως), η ίδια η τεχνική εισάγει μια κατά προσέγγιση εκτίμηση (averaging).
Ο θόρυβος της δέσμης φωτός
Σε συστήματα τριγωνοποίησης κοντινών αποστάσεων, η ακρίβεια των δεδομένων εξαρτάται σε μέγιστο βαθμό από την ορθή ερμηνεία της θέσης της ακτίνας λέιζερ. Η δέσμη φωτός δημιουργεί ένα Gaussian προφίλ πάνω στην επιφάνεια του αντικειμένου [
7]. Πιο συγκεκριμένα, η χωρική κατανομή της δέσμης φωτός σε ένα σημείο έχει ως αποτέλεσμα την εμφάνιση καταστροφικών παρεμβολών που περιορίζουν τη δυνατότητα ανάκτησης της δέσμης από τους οπτικούς αισθητήρες. Το φαινόμενο αυτό είναι γνωστό και ως speckle effect και εμφανίζεται με την μορφή τυχαίας διάχυσης της δέσμης. Υπεύθυνη για το θόρυβο είναι μεταξύ άλλων η επιφάνεια του αντικειμένου και, κυρίως, η τραχύτητα της. Ο θόρυβος αυτός (speckle noise) ο οποίος εμφανίζεται στη δέσμη του φωτός μεταφέρεται και στα τελικά δεδομένα (Εικόνα 16).
Πολλοί ερευνητές έχουν μελετήσει τις συνέπειες του θορύβου στον καθορισμό αποστάσεων με τριγωνοποίηση και έχουν καταλήξει στο αξίωμα ύπαρξης ενός θεμελιώδους ορίου που αποτελεί και το φράγμα στην ακρίβεια των αποτελεσμάτων. Ο θόρυβος δύναται να μειωθεί με την εφαρμογή συγκεκριμένων τεχνικών. Οι γραμμικές τεχνικές φιλτραρίσματος που βασίζονται σε χρονικούς τελεστές και βρίσκουν εφαρμογή στην ψηφιακή επεξεργασία εικόνας δεν αποδίδουν στην συγκεκριμένη περίπτωση και δεν μπορούν να μειώσουν τέτοιου είδους θόρυβο. Η διόρθωση γίνεται με τεχνικές φιλτραρίσματος στο πεδίο της εικόνας. Τα φίλτρα αυτά είναι γνωστά από τους χώρους της ψηφιακής επεξεργασίας εικόνας και ως χωρικά φίλτρα. Μια κλασική μέθοδος για την ελαχιστοποίηση του προβλήματος ορθής ερμηνείας της θέσης, αποτελεί η εύρεση του κέντρου του μονοδιάστατου παλμού της δέσμης. Τα αποτελέσματα της τεχνικής αυτής είναι σωστά μόνο όταν η επιφάνεια σάρωσης είναι επίπεδη [
3]. Καταλήγουμε λοιπόν στον κανόνα ότι «τα οπτικά χαρακτηριστικά της επιφάνειας ενός αντικειμένου επηρεάζουν τις επιδόσεις του σαρωτή λέιζερ» [
7].
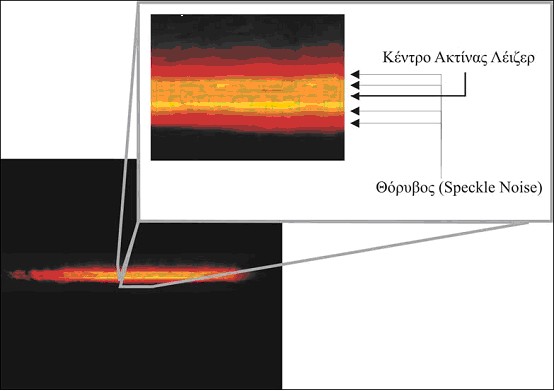
Εικόνα 16
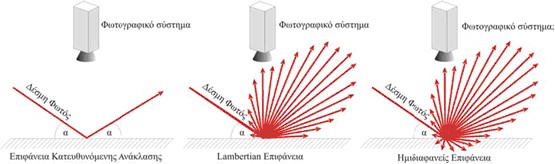
Ο βέλτιστος τύπος επιφάνειας για ψηφιοποίηση με ακτίνες λέιζερ είναι αυτός που φέρει χαρακτηριστικά Lambert (ματ) και ταυτόχρονα έχει υψηλό δείκτη ανάκλασης. Στην Εικόνα 17 περιγράφεται ο τρόπος που συμπεριφέρονται οι δέσμες φωτός καθώς ανακλώνται σε μια επιφάνεια κατευθυνόμενης ανάκλασης (specular) (Εικόνα 17α), σε μια Lambertian επιφάνεια (Εικόνα 17β) και μια ημιδιαφανή επιφάνεια (π.χ. μάρμαρο) (Εικόνα 17γ).
Εικόνα 17
Σε μια ημιδιαφανή επιφάνεια το φως διεισδύει μέσα στα υποστρώματα του αντικειμένου σε βάθος ανάλογο της ισχύος του. Επιπρόσθετα, τα φως διαχέεται μέσα στα υποστρώματα του αντικείμενου και δημιουργεί διασκορπισμό. Στην ημιδιαφανή επιφάνεια το οπτικό σύστημα του σαρωτή συλλέγει πλήθος από ανακλάσεις φωτός που περιέχουν κορυφές. Αν η ένταση της δέσμης μειωθεί, ο θόρυβος γίνεται ακόμα ποιο εμφανής και αυτό μειώνει περισσότερο την ποιότητα ανακατασκευής του τρισδιάστατου μοντέλου [
7].Γενικά, θόρυβος στα δεδομένα εμφανίζεται όταν:
- η ανακλαστικότητα της επιφάνειας ποικίλει και μεταβάλλεται
- η γεωμετρία της επιφάνειας παρεκκλίνει έντονα από επίπεδο σε επίπεδο
- η πορεία της δέσμης φωτός μέχρι τον αισθητήρα παρεμποδίζεται
- η τραχύτητα της επιφάνειας προκαλεί θόρυβο στην δέσμη φωτός
Στην Εικόνα 18 εικονίζονται κάποια κλασικά παραδείγματα όπου εμφανίζονται λάθη στον υπολογισμό της απόστασης ανάμεσα στην επιφάνεια του αντικειμένου και στην πηγή της δέσμης φωτός. Στην Εικόνα 18 θεωρούμε ότι ο αισθητήρας δέχεται μονοδιάστατες ορθογραφικές προβολές. Στην Εικόνα 18α φαίνεται πως εξαιτίας της ανάκλασης δημιουργείται ένα σημείο, το οποίο δεν ανήκει πάνω στην επιφάνεια του αντικειμένου. Στις Εικόνα 18β και Εικόνα 18γ παρουσιάζονται δύο παραδείγματα όπου οι σχηματικές διαφοροποιήσεις της επιφάνειας του αντικειμένου προκαλούν εσφαλμένες μετρήσεις. Στην Εικόνα 18δ παρουσιάζεται το φαινόμενο κατά το οποίο η γεωμετρία του αντικειμένου εμποδίζει τον αισθητήρα του σαρωτή να φτάσει στην επιφάνεια του αντικειμένου όπου ανακλάται η δέσμη. Το γεωμετρικό σφάλμα που εμφανίζεται στις δύο τελευταίες περιπτώσεις είναι παρεμφερές.
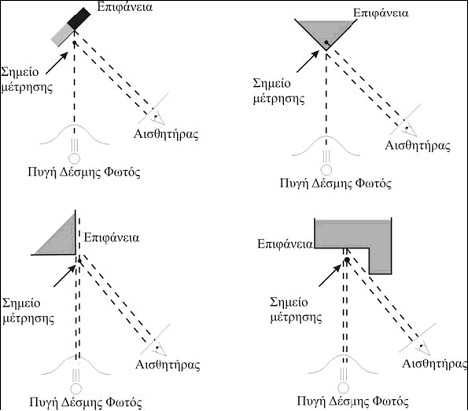
Εικόνα 18
\Ανακεφαλαιώνοντας, ο θόρυβος στην δέσμη φωτός είναι η κύρια πηγή σφαλμάτων και εμφανίζεται εξαιτίας των αντανακλάσεων της δέσμης από επιφάνειες που αποδεικνύονται τραχιές για το μήκος κύματος της δέσμης. Η τραχύτητα της επιφάνειας του αντικειμένου εισάγει τυχαίες αποκλίσεις στις διαδρομές της οπτικής πορείας (τροχιάς). Οι αποκλίσεις αυτές προκαλούν τυχαία σχήματα παραμόρφωσης στην τελική γεωμετρία. Αυτό οφείλεται στο γεγονός ότι ο παλμός της δέσμης φωτός που αποτυπώνεται στην εικόνα και χρησιμοποιείται αργότερα από τον σαρωτή για την ανάκτηση της τρίτης διάστασης (βάθος) εμπεριέχει το θόρυβο, ο οποίος επηρεάζει την αναγνώριση του κέντρου της δέσμης. Κάτι τέτοιο αποφέρει σφάλματα ακόμα και σε περιπτώσεις όπου η επιφάνεια είναι επίπεδη. Συνολικά μπορούμε να αναγνωρίσουμε τρεις διαφορετικές πηγές θορύβου που επηρεάζουν την αποτύπωση με ακτίνες λέιζερ. Αυτές οι πηγές είναι ο ηλεκτρικός θόρυβος, ο θόρυβος κβαντισμού και ο θόρυβος από τη διάχυση της δέσμης φωτός.Οι δύο πρώτες πηγές θορύβου σχετίζονται με τον αισθητήρα αποτύπωσης της εικόνας που χρησιμοποιείται. Σε περιπτώσεις όπου είναι χαμηλή η ισχύς της δέσμης φωτός, ο λόγος σήματος προς θόρυβο (signal-to-noise ratio) είναι μικρός, και έτσι, οι δύο αυτές πηγές θορύβου επηρεάζουν στο μέγιστο τα αποτελέσματα αποτύπωσης. Τέλος, ο θόρυβος από διάχυση της δέσμης σχετίζεται απόλυτα με την ίδια την φύση της ακτίνας λέιζερ [
7].
Γεωμετρική ακρίβεια και μετάδοση του θορύβου
Η γεωμετρική ακρίβεια, όπως θα δούμε και παρακάτω, δεν είναι πάντα η κυρίαρχη απαίτηση στην τεκμηρίωση των αντικειμένων πολιτιστικής κληρονομιάς. Μια μικρή απόκλιση μερικών χιλιοστών σε ένα σημείο της επιφάνειας που αποτελεί τμήμα ενός συνηθισμένου γεωμετρικού σχήματος δεν είναι πάντοτε μεγάλο πρόβλημα. Σε περιπτώσεις όπου η αποτύπωση πολύπλοκων επιφανειών είναι αναγκαία, τότε τα νέφη σημείων περιέχουν, συνήθως, θόρυβο. Ο θόρυβος παρουσιάζεται στο νέφος υπό την μορφή σημείων που ενώ θα έπρεπε να βρίσκονται πάνω στο ίδιο νοητό επίπεδο, αυτά αποκλίνουν προς τυχαίες διευθύνσεις γύρω από αυτό. Το φαινόμενο αυτό προκαλεί δυσκολίες κατά την διάρκεια της επεξεργασίας των δεδομένων αφού επιβάλουν την χρήση φίλτρων ομαλοποίησης (smoothing) και απλοποίησης (simplification). Στόχος των φίλτρων είναι να αφαιρέσουν το θόρυβο, να μειώσουν τον όγκο των δεδομένων, αλλά ταυτόχρονα, να διατηρήσουν άθικτα τα περιθώρια των επιφανειών και τον όγκο του αντικειμένου.
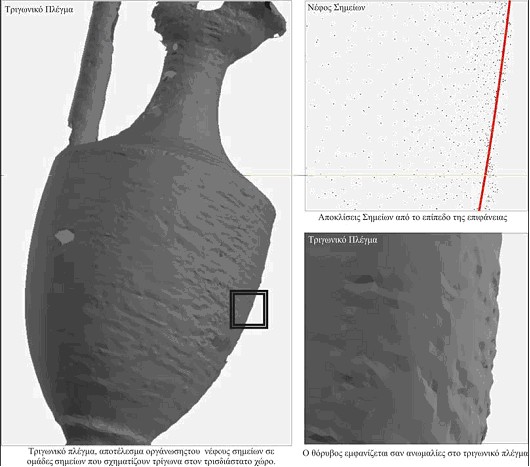
Εικόνα 19
Στην Εικόνα 19 παρουσιάζεται το τριγωνικό πλέγμα που δημιουργήθηκε από το μετασχηματισμό ενός νέφους σημείων. Το πολυγωνικό πλέγμα αναπαριστά τμήμα μιας οινοχόης που ψηφιοποιήθηκε με σαρωτή λέιζερ9. Το βάθος πολλών σημείων υπολογίσθηκε εσφαλμένα λόγω της ανακλαστικής επιφάνειας του αντικειμένου, της χρωματικής ποικιλίας που περιέχει η διακόσμηση του και του θορύβου από τη διάχυση της δέσμης. Οι επιδόσεις του συγκεκριμένου συστήματος με βαθμονόμηση μεγαλύτερης ακρίβειας και μεταβλητή ρύθμιση της έντασης της δέσμης φωτός μπορούν να είναι καλύτερα αλλά στο συγκεκριμένο παράδειγμα εσκεμμένα οι ρυθμίσεις προκάλεσαν υψηλό θόρυβο, ώστε να γίνεται αισθητό το φαινόμενο της απόκλισης σημείων. Στην ίδια εικόνα προβάλλεται επίσης και τμήμα από το νέφος σημείων. Η κόκκινη γραμμή αναπαριστά το νοητό επίπεδο της επιφάνειας της οινοχόης από την συγκεκριμένη οπτική γωνία. Τα σημεία που βρίσκονται έξω από αυτό το νοητό επίπεδο εμπεριέχουν θόρυβο. Κύρια πηγή θορύβου είναι η χρωματική πληροφορία της επιφάνειας του αντικειμένου η οποία επηρεάζει τις μετρήσεις του συστήματος που στην συγκεκριμένη περίπτωση ήταν βαθμονομημένο για την γεωμετρική αποτύπωση αντικειμένων που η επιφάνεια τους δεν φέρει χρωματικές μεταβολές. Χωρίς την χρήση αλγορίθμων ομαλοποίησης ο θόρυβος αυτός εμφανίζεται εντονότατα και στο τριγωνικό πλέγμα (αφού αυτό προήλθε από μετασχηματισμό του νέφος σημείων). Ανάλογα με το μετασχηματισμό που εφαρμόζεται ο θόρυβος γίνεται λιγότερο ή περισσότερο αισθητός. Πολλές φορές εμφανίζεται και με την μορφή γεωμετρικών ασυνεχειών στο πλέγμα.
 Digitech III-2
Digitech III-2


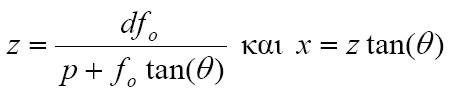
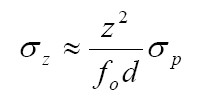
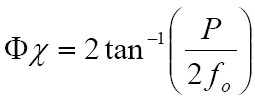 όπου P είναι το μήκος της απόστασης θέσης του αισθητήρα.
όπου P είναι το μήκος της απόστασης θέσης του αισθητήρα.